NÚMEROS COMPLEJOS. Conceptos básicos.
Breve historia.
El origen y evolución de los números complejos se originan por la necesidad de encontrar la raíz par de un número negativo en las resoluciones de ecuaciones cuadráticas. La primera referencia conocida a raíces cuadradas de números negativos proviene del trabajo de los matemáticos griegos, como Herón de Alejandría en el siglo I antes de Cristo, como resultado de una imposible sección de una pirámide.
Los complejos se hicieron más patentes en el Siglo XVI, cuando la búsqueda de fórmulas que dieran las raíces exactas de los polinomios de grados dos y tres fueron encontradas por matemáticos italianos como Tartaglia, Cardano.
Aunque sólo estaban interesados en las raíces reales de este tipo de ecuaciones, se encontraban con la necesidad de lidiar con raíces de números negativos. El término imaginario para estas cantidades fue acuñado por Descartes en el Siglo XVII y está en desuso.
La existencia de números complejos no fue completamente aceptada hasta la interpretación geométrica que fue descrita por Wessel en 1799 y redescubierta algunos años después y popularizada por Gauss. La implementación más formal, con pares de números reales fue dada en el Siglo XIX.
Los números complejos se utilizan en todos los campos de las matemáticas, en muchos de la física, con gran aplicación en la mecánica cuántica y en ingeniería, especialmente en la electrónica y las telecomunicaciones.
Se aplican en la resolución de problemas para el estudio de las funciones. Sin los números complejos, no tendría resultados "bellos y simétricos" en la búsqueda de soluciones a polinomios en una variable, tampoco se tendría la excelente extensión de la exponenciación del número "\(e\)" a exponentes complejos, y la notable relación de Euler, que une la exponenciación con las funciones trigonométricas.
Concepto de número complejo.
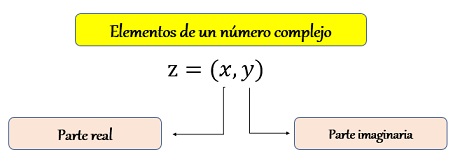
Un número complejo es un par ordenado de números reales \((x,y)\) sujeto a las operaciones de adición y multiplicación definidas especialmente como sigue:
\(\textcolor{#ff0080}{D_f}.:\) Adición de complejos,
$$(a,b)+(c,d)=(a+c,\ b+d)$$
esto es "primera más primera, segunda más segunda"
\(\textcolor{#ff0080}{D_f}.:\) Producto de complejos, $$(a,b)(c,d)=(ac-bd,\ ad+bc)$$ esto es "primera por primera menos segunda por segunda, primera por segunda más segunda por primera"
No sienta estrés debido a estas definiciones, ya verá que en el análisis complejo no es muy necesario recordar estas definiciones, sin embargo, son necesarias para el rigor matemático de las cosas, y para crear la base fundamental que ahorrará tiempo y esfuerzo al realizar cálculos.
Ahora con la finalidad de hacer más simple la comprensión del lector y de ir creando la estructura matemática que sirva de apoyo en la realización de los cálculos se define el número complejo \(z\) en forma de par ordenado como \(z=(x,y)\) donde \(x\) es la parte real y \(ye\) es la parte "imaginaria".
Operaciones de complejos con segundas coordenadas cero.
Sea \(z_1=(a,\ 0)\) y \(z_2=(c,\ 0)\) de la definición de adición de complejos se tiene:
$$z_1+z_2=(a,0)+(c,0)=(a+c,\ 0+0),\ \mathrm{entonces}~~ z_1+z_2=(a+c,0).$$
De la definición del producto de complejos,
$$z_1z_2=(a,\ 0)(c,\ 0)=(ac-0,\ 0+0)=(ac,0),$$
estos resultados conducen a la siguiente conclusión "la suma o producto de dos complejos con segunda coordenada cero, es la suma o producto de sus partes reales", pero dado que la suma o producto de dos números reales es otro número real, se tiene la afirmación:
\(\textcolor{#ff0080}{A_1}:\) Todo complejo de la forma \(\left(a,\ 0\right)=a\) donde \(a\in \mathbb{R}\)
Definición de unidad imaginaria.
El principal concepto de los números complejos es la unidad imaginaria \(i\) la cual se define como el par ordenado \((0,1).\)
Unidad imaginaria \(i.\)
$$\textcolor{#ff0080}{D_f}:\ \ \ i=\left(0,\ 1\right).$$
Si \(n\) es un número real cualquiera de la afirmación \(A_1\) se puede escribir \(n=(n,0)\) y el producto \(ni=\left(n,\ 0\right)\cdot\left(0,\ 1\right)=\left(0-0,n+0\right)=(0,n)\) de dónde se tiene la siguiente afirmación:
\(\textcolor{#ff0080}{A_2}:\) Todo complejo de la forma \(ni=\left(0,\ n\right).\)
A partir de las afirmaciones \(A_1\) y \(A_2\) y de las definiciones del suma y producto de números complejos y de la unidad imaginaria \(i,\) se construye todo el andamiaje matemático de los números complejos. Debido a su gran importancia estos resultados se resumen en la tabla siguiente:
Fundamentos analíticos de los números complejos.
1. \(\textcolor{#ff0080}{D_f}:\) Adición de complejos, \(\left(a,b\right)+\left(c,d\right)=\left(a+c,\ b+d\right)\)
2. \(\textcolor{#ff0080}{D_f}:\) Producto de complejos, \((a,b)(c,d)=(ac-bd,\ ad+bc)\)
3. \(\textcolor{#ff0080}{D_f}:\ \ \ i=\left(0,\ 1\right)\)
4. \(\textcolor{#ff0080}{A_1}:\) Todo complejo de la forma \(\left(a,\ 0\right)=a\)
5. \(\textcolor{#ff0080}{A_2}:\) Todo complejo de la forma \(ni=\left(0,\ n\right).\)
Un resultado importante.
Primer resultado. De las definiciones del producto de dos complejos y de la unidad imaginaria se tiene,
\begin{align}
&i^2=i\cdot i\\
&i^2=\left(0,\ 1\right)\left(0,\ 1\right)\\
&i^2=\left(0-1,\ 0+0\right)\\
&i^2=(-1,\ 0)\end{align}
pero por la afirmación \(A_1\) el par \(\left(-1,\ 0\right)=-1\) y de aquí el resultado \(R_1: i^2=-1.\)
Muchas personas tienden a definir de manera errónea la unidad imaginaria como \(i=\sqrt{-1}\) sin embargo, esta no es la definición de la unidad imaginaria, sino más bien una consecuencia analítica cuando se aplica al resultado \(i^2=-1\) el axioma de las igualdades, tomando raíz cuadrada en ambos miembros como se ve a continuación, \begin{align}i^2&=-1\\ \sqrt{i^2}&=\sqrt{-1}\Longrightarrow\left|i\right|=\sqrt{-1}\end{align} lo cual comúnmente es expresado comunmente como \(i=\sqrt{-1}\) para \(|i|>0\) lo cual es una media verdad. Al estudiar las raíces de un número complejo se verá que \(\sqrt{-1}=\pm i\) que es la historia completa, sin embargo, recordar el resultado \(i^2=-1\) tiene mucha utilidad como se verá a largo del estudio de los complejos.
Representación de un número complejo.
Como ya se ha dicho un número complejo es un par ordenado escrito en la forma \(z=\left(x,y\right)\) donde \(x\) es la parte real y ye es la parte imaginaria, sin embargo, además de la forma de par ordenado un número complejo puede ser representado en otras formas, como se muestra a continuación.
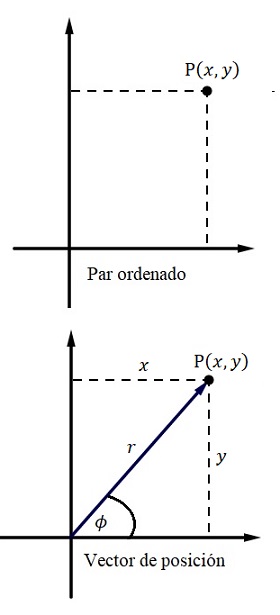
1. Par Ordenado \((x,y).\)
2. Forma binómica \(z=x+yi.\) Donde si \(y=0\) el número complejo se reduce a un número real ya que \(x+0i=x\) por la afirmación \(A_1\). Si \(x=0\) el número complejo se reduce a \(yi,\) por \(A_2\) y se dice que es un número imaginario puro.
3. Vector de posición: un vector es un ente matemático que diene módulo, dirección y sentido, el complejo \(z=(x,y)\) también puede ser representado como un vector de posición que tiene su afijo en origen de coordenadas \((0,0)\) donde el eje de abscisas es el eje real \((\mathbb{R})\) y el eje de ordenadas es el imaginario \((I_m),\)como muestra la figura. Note que \(r\) es la hipotenusa del triángulo, por tanto, cumple con el teorema de Pitágoras \(r^2=x^2+y^2.\) El ángulo \(\theta\) medido en sentido positivo es el argumento principal de \(z,\) y \(\left|z\right|=r\) es su módulo.
4. Forma polar. Esta forma conocida también como la forma trigonométrica de \(z\) permite escribir al complejo \(z\) en función de su módulo y el ángulo \(\phi\) (menor ángulo que forma el vector de posición que representa al complejo y el eje horizontal positivo llamado también eje real) esto es \(z=re^{i\phi}\) para \(r\) igual al módulo y \(\phi\) el argumento principal
Segundo resultado. Por propiedades de radicales si \(a\) y \(b\) son positivos se escribe \(\sqrt{a\cdot b}=\sqrt a\cdot\sqrt b\) para \(\sqrt{-x}\) se tiene, $$\sqrt{-x}=\sqrt x\sqrt{-1}\ =\sqrt x\cdot i$$ con lo cual queda resuelto el problema de la raíz par de un número negativo, al trabajar en el campo de lo complejos, como verá más adelante al trabajar raíces complejas.
Para más contenidos y luego clic en la pestaña del contenido deseado.
Clasificación de números complejos
Igualdad de complejos.
Dos números complejos son iguales cuando tienen la misma componente real y la misma componente imaginaria.
Así si \(z_1=a+bi\) y \(z_2=c+di\) son iguales entonces se tiene,
\(z_1=z_2\ \ \Longleftrightarrow\ a=b\ \ \land\ c=d\)
Complejos opuestos y conjugados.
Complejos opuestos: Se dice que los complejos \(z_1\) y \(z_2\) son complejos opuestos cuando sus partes reales e imaginarias que son inversos aditivos, esto es \(z_1=x+yi\) y \(z_2=-x-yi,\) mientras que si \(z_1=x+yi,\) al complejo cuya parte imaginaria es inversa aditiva a la parte imaginaria de \(z_1\) se le llama complejo conjugado de \(z_1\) lo cual se denota por \(\overline{z}=x-yi.\) Para dos complejos conjugados cualesquiera \(z_1\) y \(z_2\) se cumplen las propiedades siguientes:
$$\begin{array}{l}
\textcolor{#ff0080}{1}.~~ \overline{z_1\pm z_2}=\overline{z_1}\pm\overline{z_2}&\textcolor{#ff0080}{3}.~~\overline{\left(\frac{z_1}{z_2}\right)}=\frac{\overline{z_2}}{\overline{z_2}}\\
\textcolor{#ff0080}{ 2}.~~\ \ \overline{z_1z_2}=\overline{z_1}\cdot\overline{z_2}~~~~~&\textcolor{#ff0080}{4}.~~\ \ \overline{\overline{z_1}}=z~~~~~~\\
\end{array}$$
Ejemplo. Dado el complejo \(z=3+5i\) escribir su conjugado y su opuesto y compruebe la propiedad cuatro de arriba.
Solución: el conjugado \(\overline{z}=3-5i,\) para el opuesto \(z_o=-3-5i.\) Para comprobar la propiedad basta con determinar el conjugado de \(\overline{z}=3-5i\) que es \(z=3+5i\)
Para las demostraciones de las primeras tres propiedades se deberá esperar hasta el estudio de las operaciones con complejos, las cuales se presentan en la sección siguiente.
Note que, la única diferencia entre dos complejos conjugados es que la parte imaginaria de uno es el inverso aditivo del otro. De la afirmación \(A_1\) todo complejo de la forma \(\left(n,\ 0\right)=n\) (la parte imaginaría es nula y por tal razón no tiene inverso aditivo) y de esto se deduce que el conjugado de un número real es el mismo número real.